题目内容
求y=sin(
-x)-cos2(
+x)+2的值域.
| π |
| 4 |
| π |
| 4 |
考点:二倍角的余弦,三角函数中的恒等变换应用
专题:三角函数的求值
分析:利用诱导公式化简函数的解析式为y=-[sin(
-x)-
]2+
,根据sinx的范围,利用二次函数的性质求得函数的值域.
| π |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
解答:
解:y=sin(
-x)-cos2(
+x)+2=sin(
-x)-sin2(
-x)+2=-[sin(
-x)-
]2+
,
故当sin(
-x)=
时,函数y取得最大值为
,当sin(
-x)=-1时,函数y取得最小值为0,
故函数的值域为[0,
].
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
故当sin(
| π |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| π |
| 4 |
故函数的值域为[0,
| 9 |
| 4 |
点评:本题主要考查诱导公式、正弦函数的定义域和值域,二次函数的性质的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在(-π,4π)内与-
终边相同的角有( )个.
| 5π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
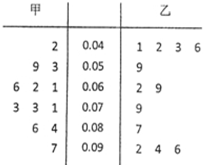 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,则甲、乙两地浓度的方差较小的是
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,如图是根据某地某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,则甲、乙两地浓度的方差较小的是
