题目内容
下列命题正确的是( )
| A、?x∈R,都有x2-3x+3>0成立 |
| B、?x0∈R,使sin2x0+cos2x0<1成立 |
| C、“?x0∈R,使x02-1<0”的否定是“?x∈R,都有x2-1>0” |
| D、若“p∨q”为假,则命题p、q中一个真另一个假 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:由方程x2-3x+3=0的判别式小于0说明A正确;结合三角函数的平方关系说明B错误;
写出命题的否定说明C错误;由复合命题的真值表说明D错误.
写出命题的否定说明C错误;由复合命题的真值表说明D错误.
解答:
解:对于A,∵方程x2-3x+3=0的判别式△=(-3)2-4×1×3=-3<0,
∴?x∈R,都有x2-3x+3>0成立,A正确;
对于B,由同角三角函数的基本关系式可知,?x0∈R,使sin2x0+cos2x0<1成立,B正确;
对于C,“?x0∈R,使x02-1<0”的否定是“?x∈R,都有x2-1≥0”,C错误;
对于D,若“p∨q”为假,则命题p、q中至少有一个假,D错误.
故选:A.
∴?x∈R,都有x2-3x+3>0成立,A正确;
对于B,由同角三角函数的基本关系式可知,?x0∈R,使sin2x0+cos2x0<1成立,B正确;
对于C,“?x0∈R,使x02-1<0”的否定是“?x∈R,都有x2-1≥0”,C错误;
对于D,若“p∨q”为假,则命题p、q中至少有一个假,D错误.
故选:A.
点评:本题考查了命题的真假判断与应用,考查了复合命题的真假判断,考查了命题的否定,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}中,a1=1,a2n=n-an,a2n+1=an+1,则a100=( )
| A、30 | B、31 | C、32 | D、33 |
某程序框图如图所示,则输出的S的值为( )


| A、11 | B、19 | C、26 | D、57 |
曲线y=ex与直线y=5-x交点的纵坐标在区间(m,m+1)(m∈Z)内,则实数m的值为( )
| A、1 | B、2 | C、3 | D、4' |
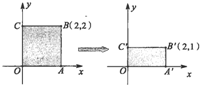 已知矩阵M=
已知矩阵M=