题目内容
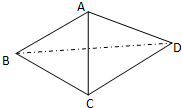 如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2| 3 |
考点:轨迹方程
专题:计算题,空间位置关系与距离
分析:确定AD⊥平面ABC,在平面ABC内,取点P,连PA,则∠DPA是DP与平面ABC所成角,可得点P在△ABC内所成的轨迹是以A为圆心,半径为2的圆的一部分,即可求出点P在△ABC内所成的轨迹的长度.
解答:
解:因为∠BAD=90°,所以AD⊥AB,又AD⊥BC,且AB∩BC=B,所以AD⊥平面ABC.在平面ABC内,取点P,连PA,则∠DPA是DP与平面ABC所成角.
又因为AD=4,所以直线DP与平面ABC所成角的正切值为2,须AP=2,即点P在△ABC内所成的轨迹是以A为圆心,半径为2的圆的一部分.
而∠BAC=120°=
,故点P在△ABC内所成的轨迹的长度为
×2=
.
故答案为:
.
又因为AD=4,所以直线DP与平面ABC所成角的正切值为2,须AP=2,即点P在△ABC内所成的轨迹是以A为圆心,半径为2的圆的一部分.
而∠BAC=120°=
| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
故答案为:
| 4π |
| 3 |
点评:本题主要考查立体几何中的垂直关系,角的计算,圆的定义,扇形弧长公式.

练习册系列答案
相关题目