题目内容
设m,n是不同的直线,α,β,γ是不同的平面,则下列四个命题,其中正确命题的序号是 .
①若α∥β,m?α,则m∥β;
②若m∥α,n?α,则m∥n;
③若α⊥β,β⊥γ,则α∥γ或α⊥γ;
④若m⊥α,m∥β,则α⊥β.
①若α∥β,m?α,则m∥β;
②若m∥α,n?α,则m∥n;
③若α⊥β,β⊥γ,则α∥γ或α⊥γ;
④若m⊥α,m∥β,则α⊥β.
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①若α∥β,m?α,则由直线与平面平行的判定定理得m∥β,故①正确;
②若m∥α,n?α,则m与n平行或异面,故②错误;
③若α⊥β,β⊥γ,则α与γ相交或平行,故③错误;
④若m⊥α,m∥β,则由平面与平面垂直的判定定理得α⊥β,故④正确.
故答案为:①④.
②若m∥α,n?α,则m与n平行或异面,故②错误;
③若α⊥β,β⊥γ,则α与γ相交或平行,故③错误;
④若m⊥α,m∥β,则由平面与平面垂直的判定定理得α⊥β,故④正确.
故答案为:①④.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
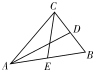 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E分别是BC、AB的中点,P是△ABC(包括边界)内任一点,则| AD |
| EP |
| A、[-7,7] |
| B、[-8,8] |
| C、[-9,9] |
| D、[-10,O] |
有一个几何体的三视图如下图所示,这个几何体应是一个( )

| A、棱锥 | B、圆锥 | C、圆柱 | D、棱柱 |
点F1,F2为椭圆
+
=1(a>b>0)的左右焦点,若椭圆上存在点A使△AF1F2为正三角形,那么椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是
某校举行演讲比赛,9位评委给选手A打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是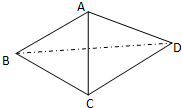 如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2