题目内容
已知f(x)=x3-3x2+2x+a,若f(x)在R上的极值点分别为m,n,则m+n= .
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:求出函数的导数,由极值的定义,结合韦达定理,即可得到m+n.
解答:
解:f(x)=x3-3x2+2x+a的导数为
f′(x)=3x2-6x+2,
由f(x)在R上的极值点分别为m,n,
则有m,n是方程3x2-6x+2=0的两个根,
由韦达定理,可得,m+n=-
=2.
故答案为:2.
f′(x)=3x2-6x+2,
由f(x)在R上的极值点分别为m,n,
则有m,n是方程3x2-6x+2=0的两个根,
由韦达定理,可得,m+n=-
| -6 |
| 3 |
故答案为:2.
点评:本题考查导数的运用:求极值,考查韦达定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知f(x)=
x3-
x2-2x+1,则该函数的单调递增区间为( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(-∞,-1) |
| B、(2,+∞) |
| C、(-1,2) |
| D、(-∞,-1)和(2,+∞) |
有一个几何体的三视图如下图所示,这个几何体应是一个( )

| A、棱锥 | B、圆锥 | C、圆柱 | D、棱柱 |
点F1,F2为椭圆
+
=1(a>b>0)的左右焦点,若椭圆上存在点A使△AF1F2为正三角形,那么椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若loga3<logb3<0,则( )
| A、0<a<b<1 |
| B、0<b<a<1 |
| C、a>b>1 |
| D、b>a>1 |
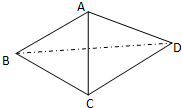 如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2
如图所示的三棱锥A-BCD中,∠BAD=90°,AD⊥BC,AD=4,AB=AC=2