题目内容
13．（1）若sin2α＞0，cosα＜0，试确定α所在象限．（2）已知θ为第三象限角，判定sin（cosθ）•cos（sinθ）的值的符号．
分析 （1）由sin2α＞0，确定α的正弦与余弦函数值的符号相同，根据余弦值小于0确定α的象限范围．
（2）先根据角的象限可以判定题中出现的sinθ、cosθ的值的范围，然后再根据sin（cosθ）•cos（sinθ）把内层的sinθ、cosθ看成弧度制表示的角即可判断符号．
解答 解：（1）∵sin2α＞0，cosα＜0，
∴2sinαcosα＞0，
∴sinα＜0，
∴α在第三、四象限
又∵cosα＜0，
∴α在第三象限．
（2）∵θ是第三象限角，
∴-1＜cosθ＜0，-1＜sinθ＜0，即cosθ与sinθ可看成一个第四象限的角．
∴sin（cosθ）＜0，cos（sinθ）＞0．
∴sin（cosθ）•cos（sinθ）＜0．
点评 本题考查象限角、轴线角，二倍角的正弦，考查分析问题解决问题的能力，是基础题．
练习册系列答案
相关题目
3．若函数f（x）=sin2xcosφ+cos2xsinφ（0＜φ＜$\frac{π}{2}$），且f（x）≤f（$\frac{2π}{9}$），则φ的值为（ ）
| A． | $\frac{2π}{9}$ | B． | $\frac{π}{9}$ | C． | $\frac{π}{18}$ | D． | $\frac{π}{36}$ |
12．已知A（1，2，-1），B（5，6，7），则直线AB与平面xoz交点的坐标是（ ）
| A． | （0，1，1） | B． | （0，1，-3） | C． | （-1，0，3） | D． | （-1，0，-5） |
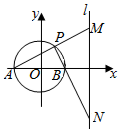已知圆O的直径AB=4，定直线l到圆心的距离为6，且直线l⊥直线AB．点P是圆上异于A、B的任意一点，直线PA、PB分别交l于M、N点．如图，以AB为x轴，圆心O为原点建立平面直角坐标系xOy．