题目内容
4.已知关于x的一元二次方程x2+2ix+(a+1)=0有实数解,则实数a的取值范围是{-1}.分析 设有实数根x0,则${{x}_{0}}^{2}+2i{x}_{0}+(a+1)=0$,由此能求出实数a的取值范围.
解答 解:∵关于x的一元二次方程x2+2ix+(a+1)=0有实数解,
∴设有实数根x0,
则${{x}_{0}}^{2}+2i{x}_{0}+(a+1)=0$,
∴$\left\{\begin{array}{l}{{{x}_{0}}^{2}+a+1=0}\\{2{x}_{0}=0}\end{array}\right.$,
解得x0=0,a=-1,
∴实数a的取值范围是{-1}.
故答案为:{-1}.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意根的判别式的合理运用.

练习册系列答案
相关题目
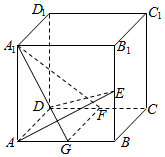 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.