题目内容
18.已知函数f(x)=a+$\frac{2}{{2}^{x}+1}$(x∈R)是奇函数.(1)求常数a的值;
(2)若f(x)>0,求x的取值范围.
分析 (1)根据函数是奇函数,则f(0)=0,建立方程即可得到结论.
(2)根据指数函数的单调性解不等式即可.
解答 解:(1)∵函数f(x)=a+$\frac{2}{{2}^{x}+1}$(x∈R)是奇函数.
∴f(0)=0,即f(0)=a+1=0,得a=-1.
(2)∵a=-1.
∴f(x)=-1+$\frac{2}{{2}^{x}+1}$,
由f(x)=-1+$\frac{2}{{2}^{x}+1}$>0得$\frac{2}{{2}^{x}+1}$>1,
即2x+1<2,即2x<1,
即x<0,
即x的取值范围是(-∞,0).
点评 本题主要考查函数奇偶性的应用以及不等式的求解,利用奇函数f(0)=0的性质是解决本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
8.记a=sin(cos2016°),b=sin(sin2016°),c=cos(sin2016°),d=cos(cos2016°),则( )
| A. | d>c>b>a | B. | d>c>a>b | C. | c>d>b>a | D. | a>b>d>c |
6.已知A,B两地间的距离为20km,B,C两地间的距离为40km,现测得∠ABC=120°,则A,C两地间的距离为( )
| A. | 20km | B. | 20$\sqrt{3}$km | C. | 20$\sqrt{5}$km | D. | 20$\sqrt{7}$km |
3.设函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}}&{x<0}\\{1+2x}&{x≥0}\end{array}\right.$,则f(2)-f(-2)的值是( )
| A. | -$\frac{11}{4}$ | B. | 1 | C. | $\frac{19}{4}$ | D. | $\frac{21}{4}$ |
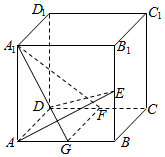 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.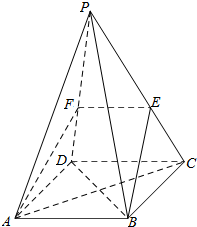 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PB=PD,过AB的平面分别交棱PC,PD于点E,F.