题目内容
1.若实数(a>0,b>0),且$\frac{1}{a}$+$\frac{2}{b}$=1,则当$\frac{2a+b}{8}$的最小值为m,函数f(x)=e-mx|lnx|-1的零点个数为1.分析 由基本不等式求最值可得m值,问题转化为两函数图象交点个数问题,由指数函数和对数函数的图象特点可得.
解答 解:∵实数(a>0,b>0),且$\frac{1}{a}$+$\frac{2}{b}$=1,
∴$\frac{2a+b}{8}$=$\frac{1}{8}$(2a+b)($\frac{1}{a}$+$\frac{2}{b}$)
=$\frac{1}{8}$(4+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{1}{8}$(4+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$)=1,
当且仅当$\frac{b}{a}$=$\frac{4a}{b}$即a=2且b=4时,$\frac{2a+b}{8}$的最小值m=1,
故函数的零点个数即为函数e-x|lnx|-1=0的根的个数,
即|lnx|=ex根的个数,即函数y=|lnx|和y=ex图象交点的个数,
由指数函数和对数函数的图象特点可得两图象的交点个数为1,
故答案为:1.
点评 本题考查基本不等式求最值,涉及函数零点的个数判断,属中档题.

练习册系列答案
相关题目
6.已知A,B两地间的距离为20km,B,C两地间的距离为40km,现测得∠ABC=120°,则A,C两地间的距离为( )
| A. | 20km | B. | 20$\sqrt{3}$km | C. | 20$\sqrt{5}$km | D. | 20$\sqrt{7}$km |
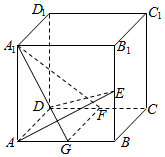 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.