题目内容
3.若函数f(x)=sin2xcosφ+cos2xsinφ(0<φ<$\frac{π}{2}$),且f(x)≤f($\frac{2π}{9}$),则φ的值为( )| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{18}$ | D. | $\frac{π}{36}$ |
分析 利用两角和的正弦函数公式化简函数解析式可得f(x)=sin(2x+φ),由f(x)≤f($\frac{2π}{9}$),可得sin($\frac{4π}{9}$+φ)=1,结合范围0<φ<$\frac{π}{2}$,由正弦函数的图象和性质可得φ的值.
解答 解:∵f(x)=sin2xcosφ+cos2xsinφ=sin(2x+φ),
∴由f(x)≤f($\frac{2π}{9}$),可得:sin(2x+φ)≤sin($\frac{4π}{9}$+φ),
∵sin(2x+φ)≤1,0<φ<$\frac{π}{2}$,x∈R,
∴sin($\frac{4π}{9}$+φ)=1,可得:$\frac{4π}{9}$+φ=2kπ+$\frac{π}{2}$,k∈Z,解得:φ=2kπ+$\frac{π}{18}$,k∈Z,
∴由0<φ<$\frac{π}{2}$,可得:φ=$\frac{π}{18}$.
故选:C.
点评 本题主要考查了三角函数恒等变换的应用,考查了正弦函数的图象和性质的应用,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
13.生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半.”这就是著名的欧拉线定理.设△ABC中,设O、H、G分别是外心、垂心和重心,下列四个选项锥误的是( )
| A. | HG=2OG | B. | $\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$ | ||
| C. | 设BC边中点为D,则有AH=3OD | D. | S△ABG=S△BCG=S△ACG |
8.记a=sin(cos2016°),b=sin(sin2016°),c=cos(sin2016°),d=cos(cos2016°),则( )
| A. | d>c>b>a | B. | d>c>a>b | C. | c>d>b>a | D. | a>b>d>c |
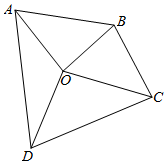 如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.
如图,为了测量学校操场四边形ABCD的周长和面积,在操场中间取一点O.测得OA=40m,OB=37m,OC=42m,OD=44m,且∠DOA=120°,∠AOB=80°,∠BOC=60°,∠COD=100°.