Question

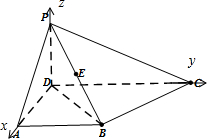
如图，在四棱椎P-ABCD中，PD⊥平面ABCD，CD∥AB，CD⊥DA且PD=DA=AB=

1

2

DC=2．设PB中点为E．
（1）证明：平面PBD⊥平面PBC；
（2）在线段DB上是否存在一点F，使得EF⊥平面PBC？若存在，请确定点F的位置（DF的长度）；若不存在，请说明理由．
（3）求点A到平面PBC的距离．

Answer 1

考点：平面与平面垂直的判定,直线与平面垂直的判定

专题：综合题,空间位置关系与距离

分析：（1）证明BC⊥平面PBD，即可证明平面PBD⊥平面PBC；
（2）建立空间直角坐标系，利用EF⊥平面ABCD，可得

EF

•

PB

=0，

EF

•

PC

=0，即可得出结论；
（3）利用等体积法V_A-PBC=V_P-ABC，可得点A到平面PBC的距离．

解答： （1）证明：直二面角P-DC-B的平面角为∠PDA=90°，
又PD⊥DC，则PD⊥平面ABCD，所以PD⊥BC．
又在平面四边形ABCP中，由已知数据易得BD⊥BC，
而PD∩BD=D，
故BC⊥平面PBD，
因为BC?平面PBC，所以平面PBD⊥平面PBC…（4分）
（2）解：由（1）的分析易知，PD⊥DA，PD⊥DC，DC⊥DA，则以D为原点建立空间直角坐标系如图所示．结合已知数据可得A（2，0，0），B（2，2，0），C（0，4，0），P（0，0，2），
则PB中点E（1，1，1）．∵F∈平面ABCD，故可设F（x，y，0），
则

EF

=(x-1，y-1，-1)，
∵EF⊥平面ABCD，
∴

EF

•

PB

=0，

EF

•

PC

=0，又

PB

=(2，2，-2)，

PC

=(0，4，-2)，
由此解得x=y=

1

2

，即F(

1

2

，

1

2

，0)，易知这样的点F存在，且为线段BD上靠近点D的一个四等分点；即DF=

2

2

…（8分）
（3）解：等体积法∵V_A-PBC=V_P-ABC，∴

1

3

S△PBC•h=

1

3

S△ABC•2，
∴

1

2

×2

2

×2

3

h=

1

2

×2×2×2，
∴h=

6

3

…（12分）

点评：本题考查点A到平面PBC的距离，考查平面与平面垂直的判定，考查线面垂直，考查学生分析解决问题的能力，属于中档题．