题目内容
已知f（x）=sinx+f′（0）cosx，则f′（
）= ．
| π |
| 3 |
考点：导数的运算
专题：导数的概念及应用
分析：根据初等函数的导数公式，计算即可．
解答：
解：∵f（x）=sinx+f′（0）cosx，
∴f′（x）=cosx-f′（0）sinx；
当x=0时，
∴f′（0）=cos0-f′（0）sin0，
即f′（0）=1，
∴f′(
)=cos
-sin
=
-
．
故答案为：
-
．
∴f′（x）=cosx-f′（0）sinx；
当x=0时，
∴f′（0）=cos0-f′（0）sin0，
即f′（0）=1，
∴f′(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
故答案为：
| 1 |
| 2 |
| ||
| 2 |
点评：本题主要考查了三角函数的导数公式，注意符号，属于基础题．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
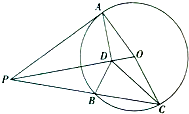如图，AP是圆O的切线，A是切点，AD⊥OP与D点，过点P作圆O的割线与圆O相交于B，C两点
如图所示，用五种不同的颜色分别给A，B，C，D四个区域涂色，相邻区域必须涂不同颜色，若允许同一种颜色多次使用，则不同的涂色方法共有
