题目内容
已知椭圆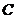 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在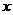 轴上,椭圆
轴上,椭圆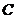 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为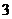 ,最小值为
,最小值为 .
.
(Ⅰ)求椭圆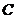 的标准方程;
的标准方程;
(Ⅱ)若直线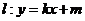 与椭圆
与椭圆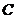 相交于
相交于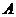 ,
,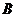 两点(
两点(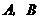 不是左、右顶点),且以
不是左、右顶点),且以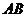 为直径的圆过椭圆
为直径的圆过椭圆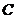 的右顶点,求证:直线
的右顶点,求证:直线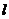 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
解:(Ⅰ)由题意设椭圆的标准方程为 ,
,
由已知得: ,
, ,
,
 ,
, ,
,
 .
.  椭圆的标准方程为
椭圆的标准方程为 .
.
(Ⅱ)设 ,
, ,
,
联立
得 ,
,

又 ,
,
因为以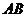 为直径的圆过椭圆的右焦点
为直径的圆过椭圆的右焦点 ,
,
 ,即
,即 ,
,
 ,
,
 ,
,
 .
.
解得:
 ,
, ,且均满足
,且均满足 ,
,
当 时,
时,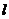 的方程为
的方程为 ,直线过定点
,直线过定点 ,与已知矛盾;
,与已知矛盾;
当 时,
时,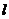 的方程为
的方程为 ,直线过定点
,直线过定点 .
.
所以,直线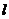 过定点,定点坐标为
过定点,定点坐标为 .
.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 ≠
≠ ,|
,| 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于
且与椭圆长轴垂直的直线交椭圆于 两点,若
两点,若 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( ) B.
B. C.
C. D.
D.
 发出的光线
发出的光线 相切,求光线
相切,求光线 表示的曲线是
表示的曲线是 被椭圆
被椭圆 所截得的线段的中点,则
所截得的线段的中点,则 B.
B.
 D.
D.
 ,
, 是函数
是函数 图象上不同于
图象上不同于 的一点.有如下结论:
的一点.有如下结论: 是等腰三角形;
是等腰三角形;