题目内容
自点 发出的光线
发出的光线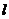 射到
射到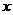 轴上,被
轴上,被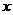 轴反射,其反射线所在直线与圆
轴反射,其反射线所在直线与圆 相切,求光线
相切,求光线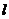 所在直线方程.
所在直线方程.
解:已知圆的标准方程是(x-2)2+(y-2)2=1,
它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1。
设光线L所在直线方程是:y-3=k(x+3)。
由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,即 .
.
整理得 解得
解得 .
.
故所求的直线方程是 ,或
,或 ,
,
即3x+4y-3=0,或4x+3y+3=0.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 B.
B.
 D.
D.

 的离心率为
的离心率为 ,则
,则 的渐近线方程为( )
的渐近线方程为( ) B.
B. C.
C. D.
D.
 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴相切,则该圆的标准方程是( ).
轴相切,则该圆的标准方程是( ). B.
B.
 D.
D.
 ,当
,当 变化时所得的直线都经过的定点为____________.
变化时所得的直线都经过的定点为____________.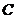 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在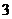 ,最小值为
,最小值为 .
.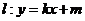 与椭圆
与椭圆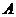 ,
,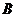 两点(
两点(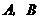 不是左、右顶点),且以
不是左、右顶点),且以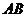 为直径的圆过椭圆
为直径的圆过椭圆 且与
且与 有相同焦点的椭圆的方程是
有相同焦点的椭圆的方程是 B.
B. C.
C. D.
D.
 ,且
,且 ,则实数
,则实数 的值为( )
的值为( )



 >
> 这五个式子中,恒成立的所有不等式的序号是________.
这五个式子中,恒成立的所有不等式的序号是________.