题目内容
已知点P0(x0,y0)在双曲线
-
=1(a>0,b>0)内,求过P0的弦中点的轨迹方程.
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设弦的两端点分别为M(x1,y1),N(x2,y2),利用点差法,求过P0的弦中点的轨迹方程.
解答:
解:设弦的端点为M(x1,y1),N(x2,y2),过P0的弦中点为(x,y),则2x=x1+x2,2y=y1+y2,
M(x1,y1),N(x2,y2),代入双曲线方程,
∴两式相减可得
-
=0,
∴
•
=
,
∴过P0的弦中点的轨迹方程为
•
=
.
M(x1,y1),N(x2,y2),代入双曲线方程,
∴两式相减可得
| 2x(x1-x2) |
| a2 |
| 2y(y1-y2) |
| b2 |
∴
| y-y0 |
| x-x0 |
| y |
| x |
| b2 |
| a2 |
∴过P0的弦中点的轨迹方程为
| y-y0 |
| x-x0 |
| y |
| x |
| b2 |
| a2 |
点评:本题考查直线与双曲线的位置关系的应用,是中档题.解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
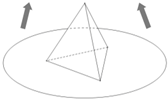 某商场为促销要准备一些正三棱锥形状的装饰品,用半径为10cm的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为xcm,体积为Vcm3.在所有能用这种包装纸包装的正三棱锥装饰品中,V的最大值是多少?并求此时x的值.
某商场为促销要准备一些正三棱锥形状的装饰品,用半径为10cm的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为xcm,体积为Vcm3.在所有能用这种包装纸包装的正三棱锥装饰品中,V的最大值是多少?并求此时x的值. 如图,在棱锥P-ABC中,PO⊥平面ABC,PA=PB=BC=3,AD=BD=1,PO=2.
如图,在棱锥P-ABC中,PO⊥平面ABC,PA=PB=BC=3,AD=BD=1,PO=2. 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=