Question

某私营企业家准备投资1320万元新办一所完全中学（含教师薪金）．对教育市场进行调查后，得到了下面的数据（以班为单位）：

学段	班 级 学生数	配 备 教师数	硬件建设 （万元）	教师年薪 （万元）
初中	40	2.5	25	3.2万元∕人
高中	45	4.0	50	4.0万元∕人

根据教育、物价、财政等部门的有关规定，在达到办学要求的前提下，初中每人每年可收取学费7000元，高中每人每年可收取学费8000元．那么第一年开办初中班和高中班各多少个，收取的学费额最多？（注：一个学校办学规模以20至30个班为宜，教师实行聘任制）

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：设出二元变量，建立约束条件和目标函数，利用线性规划的知识进行求解．

解答： 解：设开办初中班x个，高中班y个，收取的学费总额为z万元．
根据题意，有 x≥0，y≥0，且x、y∈Z；                  ①
20≤x+y≤30；                                       ②
25x+50y+2.5×3.2x+4.0×4.0y≤1320，
即 x+2y≤40．③
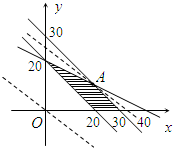
目标函数为 z=0.7×40 x+0.8×45 y=28 x+36 y，可行域如图：
把z=28 x+36 y变形为y=-

7

9

x+

z

36

，
得到斜率为-

7

9

，在y轴上的截距为

z

36

，随z
变化的一簇平行直线．由图象可以看到，当直
线z=28 x+36 y经过可行域上的点A时，z最大．
解方程组 

x+y=30 x+2y=40

得x=20，y=10，
即点A的坐标为（20，10），
所以 z_max=28×20+36×10=920．
由此可知，开办20个初中班和10个高中班，收取的学费总额最多，为920万元．

点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．