题目内容
如果(1-2x)9的展开式中第三项等于288,则
(
+
+…+
)等于( )
| lim |
| n→∞ |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点:数列的极限
专题:计算题,二项式定理
分析:由(1-2x)9的展开式中第三项等于288求出x,然后利用等比数列的求和公式求和,则
(
+
+…+
)可求.
| lim |
| n→∞ |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
解答:
解:(1-2x)9的展开式中第三项为
(-2x)2=288,解得x=
.
∴
+
+…+
=
=
=2(1-(
)n).
∴
(
+
+…+
)=
2(1-(
)n)=2.
故选:D.
| C | 2 9 |
| 3 |
| 2 |
∴
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
| ||||
1-
|
| ||||
1-
|
| 2 |
| 3 |
∴
| lim |
| n→∞ |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
| lim |
| n→∞ |
| 2 |
| 3 |
故选:D.
点评:本题考查了二项式定理,考查了等比数列的前n项和,考查了数列极限的求法,是中档题.

练习册系列答案
相关题目
下列命题正确的有( )
①(1-
)8的展开式中所有项的系数和为0;
②命题p:“?x∈R,x02-x0-1>1”的否定¬p:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,P(-1<X<0)=
-p;
④回归直线一定过样本点的中心(
,
).
①(1-
| x |
②命题p:“?x∈R,x02-x0-1>1”的否定¬p:“?x∈R,x2-x-1≤0”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,P(-1<X<0)=
| 1 |
| 2 |
④回归直线一定过样本点的中心(
. |
| x |
| y |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知点A(-1,0),B(1,0),直线y=-2x+b与线段AB相交,则实数b的取值范围是( )
| A、[-2,2] | ||||
| B、[-1,1] | ||||
C、[-
| ||||
| D、[0,2] |
下列各式正确的是( )
| A、33<30 | ||||
| B、log0.70.4<log0.70.6 | ||||
C、(
| ||||
| D、ln1.6<ln1.4 |
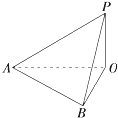 如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).
如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).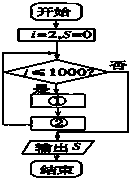 根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①
根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①