题目内容
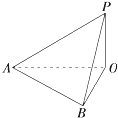 如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).
如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).考点:解三角形的实际应用
专题:应用题,解三角形
分析:分别在直角三角形AOP和直角三角形BOP中,求得OA,OB,进而在△AOB中,由余弦定理求得旗杆的高度.
解答:
解:设旗杆的高度为h,由题意,知∠OAP=30°,∠OBP=45°.
在Rt△AOP中,OA=
=
h.
在Rt△BOP中,OB=
=h.
在△AOB中,由余弦定理,
得AB2=OA2+OB2-2OA•OBcos 60°,
即202=(
h)2+h2-2
h×h×
.
解得h2=
≈176.4.
∴h≈13(m).
∴旗杆的高度约为13 m.
在Rt△AOP中,OA=
| OP |
| tan30° |
| 3 |
在Rt△BOP中,OB=
| OP |
| tan45° |
在△AOB中,由余弦定理,
得AB2=OA2+OB2-2OA•OBcos 60°,
即202=(
| 3 |
| 3 |
| 1 |
| 2 |
解得h2=
| 400 | ||
4-
|
∴h≈13(m).
∴旗杆的高度约为13 m.
点评:本题主要考查了解三角形的实际应用.考查了学生运用数学知识解决实际问题的能力.

练习册系列答案
相关题目
设Sn为等比数列{an}的前n项和,已知3S3=a4-2,3S2=a3-2,则公比q=( )
| A、3 | B、4 | C、5 | D、6 |
等差数列{an}中,a3+a13=-8,数列{bn}是等比数列,若b7=a8,则b6•b8的值为( )
| A、2 | B、4 | C、8 | D、16 |
函数y=x2+x
是( )
| 1 |
| 2 |
| A、偶函数 | B、奇函数 |
| C、既奇既偶 | D、非奇非偶 |
如果(1-2x)9的展开式中第三项等于288,则
(
+
+…+
)等于( )
| lim |
| n→∞ |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| xn |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
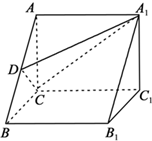 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1. 如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数为
如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数为