题目内容
13．
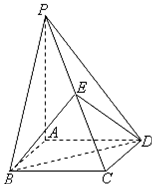如图，四边形ABCD是边长为2的菱形，∠ABC=60°，PA⊥平面ABCD，E为PC中点．求证：平面BED⊥平面ABCD．
分析 连接AC交BD于O点，连接EO，只需证明OE∥PA，得到OE⊥平面ABCD，即可得证
解答 
解：证明：连接AC交BD于O点，连接EO，
∵四边形ABCD是菱形，
∴O是AC的中点，又∵E为PC中点，
∴OE∥PA，
∵PA⊥平面ABCD，…（6分）
∴OE⊥平面ABCD，
又∵OE?平面BED，
∴平面BDE⊥平面ABCD…（12分）
点评 本题考查了空间线线、线面位置关系，属于中档题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
4．如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（ ）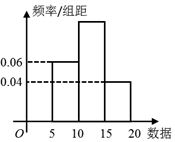
| A． | 12.5 11 | B． | 12.5 12 | C． | 12.5 13 | D． | 12.5 14 |
8．若a为实数，i为虚数单位，且$\frac{2+ai}{1+i}=3+i$，则a=（ ）
| A． | -4 | B． | -3 | C． | 3 | D． | 4 |
2．下列函数中是奇函数，且最小正周期是π的函数是（ ）
| A． | $y=cos（{\frac{3π}{2}-2x}）$ | B． | y=|cosx| | C． | $y=sin（{\frac{π}{2}+2x}）$ | D． | y=|sinx| |