题目内容
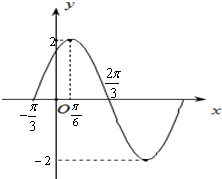 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)若f(α-
| π |
| 3 |
cos(
| ||
| cos(4π+α)sin(3π-α) |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)由图易得A=2,ω=1,结合图象过点(
,2),可得φ值,可得解析式;(2)由(1)结合f(α-
)=4cosα可得tanα=2,化简要求的式子可-tanα,可得答案.
| π |
| 6 |
| π |
| 3 |
解答:
解:(1)由图可知:A=2,
=
-(-
),
解得ω=1,∴f(x)=2sin(x+φ)
∵图象过点(
,2),∴sin(
+φ)=1,
又∵0<φ<π,∴
+φ=
,解得φ=
,
∴f(x)=2sin(x+
);
(2)由(1)知f(x)=2sin(x+
)
由f(α-
)=4cosα可得2sinα=4cosα,
∴tanα=
=2,
∴
=
=-tanα=-2
| π |
| ω |
| 2π |
| 3 |
| π |
| 3 |
解得ω=1,∴f(x)=2sin(x+φ)
∵图象过点(
| π |
| 6 |
| π |
| 6 |
又∵0<φ<π,∴
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(x+
| π |
| 3 |
(2)由(1)知f(x)=2sin(x+
| π |
| 3 |
由f(α-
| π |
| 3 |
∴tanα=
| sinα |
| cosα |
∴
cos(
| ||
| cos(4π+α)sin(3π-α) |
| sinα•(-sinα) |
| cosα•sinα |
点评:本题考查三角函数的图象和性质,涉及三角函数的恒等变换,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若6名学生排成一列,则学生甲、乙、丙三人互不相邻的排位方法种数为( )
| A、24 | B、36 | C、72 | D、144 |
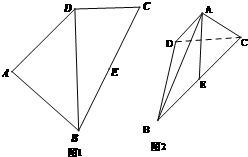 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=