题目内容
4.已知圆C1:x2+y2=4和圆2:(x-a)2+y2=4,其中a是在区间(0,6)上任意取得一个实数,那么圆C1和圆C2相交且公共弦长小于2$\sqrt{3}$的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
分析 求出满足条件的a的范围,根据区间长度之比求出满足条件的概率即可.
解答 解:a=2时,C1:x2+y2=4,C2:(x-2)2+y2=4,
那么圆C1和圆C2相交且公共弦长是2$\sqrt{3}$,
故满足条件的a的范围是:2<a<4,区间长度是2,
故在区间(0,6)上任意取得一个实数,
a在(2,4)的概率是p=$\frac{4-2}{6-0}$=$\frac{1}{3}$,
故选:D.
点评 本题考查了几何概型问题,考查圆和圆的位置关系,是一道中档题.

练习册系列答案
相关题目
14.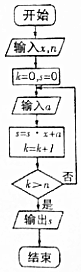 如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
 如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )| A. | 3 | B. | 10 | C. | 25 | D. | 56 |
19.天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0-9之间整数值的随机数,并制定用1,2,3,4,5表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
9.某模具长新接一批新模型制作的订单,为给订购方回复出货时间,需确定制作该批模型所花费的时间,为此进行了5次试验,收集数据如下:
(1)请根据以上数据,求关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若要制作60个这样的模型,请根据(1)中所求的回归方程预测所花费的时间.
(注:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,参考数据:$\sum_{i=1}^{5}$xiyi=12050,$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=5500)
| 制作模型数x(个) | 10 | 20 | 30 | 40 | 50 |
| 花费时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
(2)若要制作60个这样的模型,请根据(1)中所求的回归方程预测所花费的时间.
(注:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,参考数据:$\sum_{i=1}^{5}$xiyi=12050,$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=5500)
16.已知球O的半径为R,体积为V,则“R>$\sqrt{10}$”是“V>36π”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
13.抛物线y2=4x上有两点A,B到焦点的距离之和为7,则A,B到y轴的距离之和为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14.椭圆的两个焦点分别为F1(-1,0)和F2(1,0),若该椭圆与直线x+y-3=0有公共点,则其离心率的最大值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{6}$-1 | C. | $\frac{{\sqrt{6}}}{12}$ | D. | $\frac{{\sqrt{5}}}{10}$ |