题目内容
在三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,则三棱锥P-ABC的体积为( )
| A、21π | ||||
| B、12π | ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:画出图形,利用已知条件求出AB,然后求解三棱锥的体积.
解答:
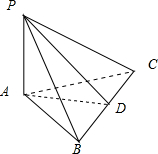 解:三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,
解:三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,
三角形PAB是直角三角形,AB=PAtan30°=3×
=
,
三角形PAC是直角三角形,AC=PAtan30°=3×
=
,
三棱锥的底面△ABC的面积为:
AB•AC•sin120°=
×
×
×
=
.三棱锥的高为PA=3,
则三棱锥P-ABC的体积为:
×
×3=
.
故选:D
 解:三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,
解:三棱锥P-ABC中,PA⊥底面ABC,∠APC=∠BPA=30°,∠BAC=120°,PA=3,三角形PAB是直角三角形,AB=PAtan30°=3×
| ||
| 3 |
| 3 |
三角形PAC是直角三角形,AC=PAtan30°=3×
| ||
| 3 |
| 3 |
三棱锥的底面△ABC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
则三棱锥P-ABC的体积为:
| 1 |
| 3 |
3
| ||
| 4 |
3
| ||
| 4 |
故选:D
点评:本题是基础题,考查三棱锥的体积的计算,注意三棱锥的特征是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知向量
,
均为单位向量,它们的夹角为600,实数x,y满足|x
+y
|=
,那么x+2y的最大值为( )
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
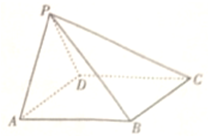 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为棱形且∠DAB= 如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为
如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为