题目内容
1．在数列{an}中，an+1-an=2，a2=5，则{an}的前4项和为（ ）| A． | 9 | B． | 22 | C． | 24 | D． | 32 |
分析 由等差数列的定义求出公差，利用等差数列的性质求和即可．
解答 解：由等差数列的性质可得an+1-an=2，可得d=2，
∴数列{an}的前4项之和S4=2（5+7）=24．
故选：C．
点评 本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
相关题目
11．已知函数f（x）=sin（2x-$\frac{π}{2}$）（x∈R）下列结论错误的是（ ）
| A． | 函数f（x）的最小正周期为π | B． | 函数f（x）是偶函数 | ||
| C． | 函数f（x）在区间[0，$\frac{π}{2}$]上是增函数 | D． | 函数f（x）的图象关于直线x=$\frac{π}{4}$对称 |
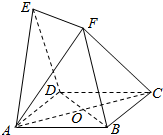如图，四边形ABCD与BDEF均为菱形，设AC与BD相交于点O，若∠DAB=∠DBF=60°，且FA=FC．
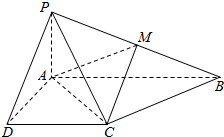已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且$PA=AD=DC=\frac{1}{2}$，AB=1，M是PB的中点．
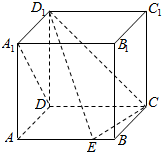如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E是棱AB上的动点．
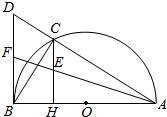如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，F为BD中点，连接AF交CH于点E，