题目内容
13.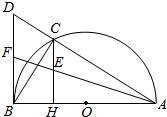 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,F为BD中点,连接AF交CH于点E,(Ⅰ)求证:∠BCF=∠CAB;
(Ⅱ)若FB=FE=1,求⊙O的半径.
分析 (Ⅰ)由AB是直径,得∠ACB=90°,由此能证明∠BCF=∠CAB.
(Ⅱ)由FC=FB=FE得:∠FCE=∠FEC,由此利用切割线定理和勾股定理能求出⊙O半径.
解答  证明:(Ⅰ)因为AB是直径,所以∠ACB=90°
证明:(Ⅰ)因为AB是直径,所以∠ACB=90°
又因为F是BD中点,所以∠BCF=∠CBF=90°-∠CBA=∠CAB
因此∠BCF=∠CAB. …(5分)
解:(Ⅱ)直线CF交直线AB于点G,
由FC=FB=FE得:∠FCE=∠FEC
所以FA=FG,且AB=BG
由切割线定理得:(1+FG)2=BG×AG=2BG2…①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2…②
由①、②得:FG2-2FG-3=0
解之得:FG1=3,FG2=-1(舍去)
所以AB=BG=2$\sqrt{2}$,
所以⊙O半径为$\sqrt{2}$.…(10分)
点评 本题考查两角相等的证明,考查圆的半径的求法,是基础题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
相关题目
4.已知表面积为24π的球体,其内接正四棱柱(底面是正方形,侧棱垂直于底面)的高为4,则这个正四棱柱的侧面积为( )
| A. | 32 | B. | 36 | C. | 48 | D. | 64 |
1.在数列{an}中,an+1-an=2,a2=5,则{an}的前4项和为( )
| A. | 9 | B. | 22 | C. | 24 | D. | 32 |
5.已知正三棱锥S-ABC中,E是侧棱SC的中点,且SA⊥BE,则SB与底面ABC所成角的余弦值为( )

| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{6}$ |
2.使不等式tanx$≥\sqrt{3}$成立的x的集合为( )
| A. | (kπ+$\frac{π}{6}$,kπ+$\frac{π}{2}$)k∈Z | B. | [kπ+$\frac{π}{6}$,kπ+$\frac{π}{2}$)k∈Z | C. | [kπ+$\frac{π}{3}$,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{3}$,kπ+$\frac{π}{2}$)k∈Z |
3.9,a,b,243是等比数列,则a,b的值分别为( )
| A. | 27,81 | B. | 81,27 | C. | -27,81 | D. | 27,-81 |
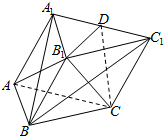 如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.
如图,已知三棱柱ABC-A1B1C1的侧面BCC1B1是菱形,D为A1C1的中点,B1C⊥A1B.