题目内容
两条直线y=kx+2k+1和x+2y-4=0的交点在第四象限,则k的取值范围是_ .
考点:两条直线的交点坐标
专题:直线与圆
分析:联立方程组可直接求出交点坐标,令交点的横坐标大于0,综坐标小于0,解不等式组即可.
解答:
解:联立
,
解得x=
,y=
.
由两直线y=kx+2k+1与x+2y-4=0交点在第四象限可得:
>0,
<0.
解此不等式组可得-
<k<-
,
∴k的取值范围为-
<k<-
.
|
解得x=
| 2-4k |
| 2k+1 |
| 6k+1 |
| 2k+1 |
由两直线y=kx+2k+1与x+2y-4=0交点在第四象限可得:
| 2-4k |
| 2k+1 |
| 6k+1 |
| 2k+1 |
解此不等式组可得-
| 1 |
| 2 |
| 1 |
| 6 |
∴k的取值范围为-
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查两条直线的交点坐标,解方程组和不等式组是解决问题的关键,属基础题.

练习册系列答案
相关题目
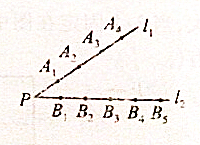 直线l1与l2相交于点P,除点P外在直线l1上还有A1,A2,A3,A4四点,在直线l2上还有B1,B2,B3,B4,B5五点,若A1,A2,A3,A4四点与B1,B2,B3,B4,B5这五点中各取一点连成一条直线,问交点的个数最多有几个.
直线l1与l2相交于点P,除点P外在直线l1上还有A1,A2,A3,A4四点,在直线l2上还有B1,B2,B3,B4,B5五点,若A1,A2,A3,A4四点与B1,B2,B3,B4,B5这五点中各取一点连成一条直线,问交点的个数最多有几个.