题目内容
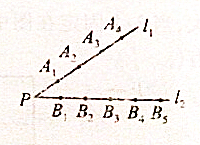 直线l1与l2相交于点P,除点P外在直线l1上还有A1,A2,A3,A4四点,在直线l2上还有B1,B2,B3,B4,B5五点,若A1,A2,A3,A4四点与B1,B2,B3,B4,B5这五点中各取一点连成一条直线,问交点的个数最多有几个.
直线l1与l2相交于点P,除点P外在直线l1上还有A1,A2,A3,A4四点,在直线l2上还有B1,B2,B3,B4,B5五点,若A1,A2,A3,A4四点与B1,B2,B3,B4,B5这五点中各取一点连成一条直线,问交点的个数最多有几个.考点:排列、组合及简单计数问题
专题:排列组合
分析:由于各点连线交点不重合,则交点最多,共分两步,第一步,从l1上的A1,A2,A3,A4四点,取两点,第二步,从l2上的B1,B2,B3,B4,B5五点,取两点,根据四边形的对角线的知识即可得到交点的个数.
解答:
解:若各点连线交点不重合,则交点最多,共分两步,
第一步,从l1上的A1,A2,A3,A4四点,取两点,有
=6种不同的取法,
第一步,从l2上的B1,B2,B3,B4,B5五点,取两点,有
=10种不同的取法,
根据分步计数原理共有6×10=60不同的取法,
而每种取法对应不同的四边形,四边形对角线有唯一的交点,
故所求的交点个数为60个,
第一步,从l1上的A1,A2,A3,A4四点,取两点,有
| C | 2 4 |
第一步,从l2上的B1,B2,B3,B4,B5五点,取两点,有
| C | 2 5 |
根据分步计数原理共有6×10=60不同的取法,
而每种取法对应不同的四边形,四边形对角线有唯一的交点,
故所求的交点个数为60个,
点评:本题的关键是将所求的交点个数转化为四边形对角线的交点问题,属于中档题

练习册系列答案
相关题目
已知下列命题:
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
①命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p或q”为假命题,则“?p且?q为真命题”;
③“a>5”是“a>2”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
| A、①②③ | B、②④ | C、②③ | D、④ |
命题“事件A与事件B互斥”是命题“事件A与事件B对立”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知复数z=
,则z-|z|对应的点所在的象限为( )
| 1 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知i是虚数单位,则复数
等于( )
| (1+i)2 |
| 1-2i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|