题目内容
已知圆C的方程为x2+y2+6x-8y=0,直线l:y=kx+2k+1.
(Ⅰ)当k=2时,求圆C关于直线l对称的圆M的方程;
(Ⅱ)求直线l被圆M截得的弦长的最大值和最小值,并求出相应的直线l的方程.
(Ⅰ)当k=2时,求圆C关于直线l对称的圆M的方程;
(Ⅱ)求直线l被圆M截得的弦长的最大值和最小值,并求出相应的直线l的方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(Ⅰ)求出圆C关于直线l对称的点的坐标,即可求出圆C关于直线l对称的圆M的方程;
(Ⅱ)当直线l过圆心M时,弦长的最大;当直线l过P且与PM垂直时,弦长最小.
(Ⅱ)当直线l过圆心M时,弦长的最大;当直线l过P且与PM垂直时,弦长最小.
解答:
解:(Ⅰ)圆C的方程为x2+y2+6x-8y=0,可化为(x+3)2+(y-4)2=25,则圆心C(-3,4),半径为5.
当k=2时,直线l:y=2x+5,
设M(a,b),则
,
∴a=1,b=2,
∴圆M的方程为(x-1)2+(y-2)2=25;
(Ⅱ)直线l的方程可化为y-1=k(x+2),恒过定点P(-2,1),在圆内.
当直线l过圆心M时,弦长的最大值为直径10,此时l的方程为y-1=
(x+2),即x-3y+5=0;
当直线l过P且与PM垂直时,弦长最小,此时|PM|=
,最小为2
=2
,l的方程为3x+y+5=0.
当k=2时,直线l:y=2x+5,
设M(a,b),则
|
∴a=1,b=2,
∴圆M的方程为(x-1)2+(y-2)2=25;
(Ⅱ)直线l的方程可化为y-1=k(x+2),恒过定点P(-2,1),在圆内.
当直线l过圆心M时,弦长的最大值为直径10,此时l的方程为y-1=
| 2-1 |
| 1+2 |
当直线l过P且与PM垂直时,弦长最小,此时|PM|=
| 10 |
| 52-10 |
| 15 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
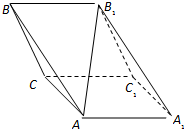 如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,