Question

已知

x-y+2≥0 x+y-4≥0 2x-y-5≤0

求：
（Ⅰ）z=x+2y-4的最大值；
（Ⅱ）z=x²+y²-10y+25的最小值；
（Ⅲ）z=

2y+1

x+1

的范围．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：（Ⅰ）作出不等式组对应的平面区域利用z=x+2y-4的几何意义，即可求最大值；
（Ⅱ）z=x²+y²-10y+25的几何意义为两点间的距离的平方；
（Ⅲ）z=

2y+1

x+1

=2•

y+ 1 2

x+1

的几何意义为两点之间斜率的取值范围．

解答： 解：（Ⅰ）作出可行域如图所示，并求出顶点的坐标A（1，3）、B（3，1）、C（7，9）．
易知可行域内各点均在直线x+2y-4=0的上方，故x+2y-4＞0，
将点C（7，9）代入z得最大值为21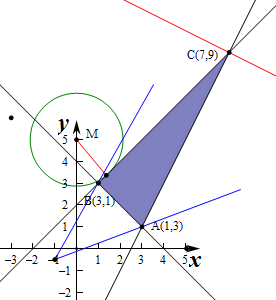．（红线部分）
（Ⅱ）z=x²+y²-10y+25=x²+（y-5）²表示可行域内任一点（x，y）到定点M（0，5）的距离的平方，
过M作直线AC的垂线，易知垂足N在线段AC上，
故z的最小值是|MN|²=

9

2

．（绿线部分）
（Ⅲ）z=

2y+1

x+1

=2•

y+ 1 2

x+1

的几何意义表示为区域内的动点P（x，y）与定点D（-1，-

1

2

）连线斜率的2倍．
由图象可知DA的斜率最小为k=

7

4

，DB的斜率最大为k=

3

8

，
即

3

8

≤k≤

7

4

，
即

3

4

≤2k≤

7

2

，（蓝色线部分）
即z的取值范围是[

3

4

，

7

2

]．

点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．要求熟练掌握常见目标函数的几何意义．