题目内容
12.为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.| 数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
| 物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
分析 (Ⅰ)做出物理和数学成绩的平均数,进而做出两门成绩的方差,把两个方差进行比较,得到物理的方差小于数学的方差,所以物理成绩更稳定.
(Ⅱ)根据上一问做出的平均数,利用最小二乘法做出线性回归方程的系数,把样本中心点代入求出a的值,写出线性回归方程;
(Ⅲ)把所给的物理的成绩代入预报出数学的成绩.
解答 解:(Ⅰ)$\overline{x}$=120,$\overline{y}$=80,
∴数学的方差是$\frac{1}{7}$(144+289+289+64+64+144)=142,
物理的方差是$\frac{1}{7}$(36+81+64+16+16+1+36)=$\frac{250}{7}$,
从而物理的方差小于数学的方差,所以物理成绩更稳定.
(Ⅱ)由于x与y之间具有线性相关关系,
∴$\widehat{b}$=$\frac{497}{994}$=0.5,$\widehat{a}$=80-0.5×120=20
∴线性回归方程为y=0.5x+20
(Ⅲ)当y=90时,x=140
即该生物理是90分时,数学成绩是140.
点评 本题考查线性回归方程的求法和应用,考查判断两组数据的稳定性的方法,本题解题的关键是正确运算出结果.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,取DE的中点F,则$\overrightarrow{AF}•\overrightarrow{BC}$的值为( )
| A. | $-\frac{5}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{11}{8}$ |
20.若${(3x-\frac{1}{{\sqrt{x}}})^n}(n∈N*)$的展开式中各项系数和为64,则其展开式中的常数项为( )
| A. | 540 | B. | -540 | C. | 135 | D. | -135 |
 我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( )
我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( )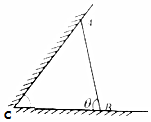 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ