题目内容
2.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作某一渐近线的垂线,分别与两渐近线相交于A,B两点,若$\frac{|AF|}{|BF|}=\frac{1}{2}$,则双曲线的离心率为2或$\frac{2\sqrt{3}}{3}$.分析 方法一、运用两渐近线的对称性和条件,可得A为BF的中点,由垂直平分线的性质和等腰三角形的性质,可得Rt△OAB中,∠AOB=$\frac{π}{3}$,求得渐近线的斜率,运用离心率公式即可得到;
方法二、设过左焦点F作$y=-\frac{b}{a}x$的垂线方程为$y=\frac{a}{b}(x+c)$,联立渐近线方程,求得交点A,B的纵坐标,由条件可得A为BF的中点,进而得到a,b的关系,可得离心率.
解答 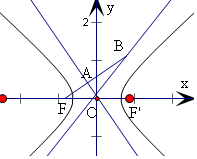 解法一:当b>a>0时,由$\frac{|AF|}{|BF|}=\frac{1}{2}$,可知A为BF的中点,由条件可得
解法一:当b>a>0时,由$\frac{|AF|}{|BF|}=\frac{1}{2}$,可知A为BF的中点,由条件可得
$\frac{|OA|}{|OB|}=\frac{1}{2}$,
则Rt△OAB中,∠AOB=$\frac{π}{3}$,
渐近线OB的斜率k=$\frac{b}{a}$=tan$\frac{π}{3}$=$\sqrt{3}$,
即离心率e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$=2.
同理当a>b>0时,可得e=$\frac{2\sqrt{3}}{3}$;
解法二:设过左焦点F作$y=-\frac{b}{a}x$的垂线方程为$y=\frac{a}{b}(x+c)$
联立$\left\{{\begin{array}{l}{y=\frac{a}{b}(x+c)}\\{y=-\frac{b}{a}x}\end{array}}\right.$,解得,${y_A}=\frac{ab}{c}$,
联立$\left\{{\begin{array}{l}{y=\frac{a}{b}(x+c)}\\{y=\frac{b}{a}x}\end{array}}\right.$,解得,yB=$\frac{abc}{{b}^{2}-{a}^{2}}$,
又$\frac{|AF|}{|BF|}=\frac{1}{2}$,∴yB=2yA∴b2=3a2,
所以离心率e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$=2.
同理当a>b>0时,可得e=$\frac{2\sqrt{3}}{3}$.
故答案为:2或$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的性质和应用,主要是离心率的求法,解题时要认真审题,仔细解答,注意向量共线的合理运用.

 名校课堂系列答案
名校课堂系列答案| 数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
| 物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)

| A. | $12+2\sqrt{2}$ | B. | $8+2\sqrt{2}$ | C. | $4+4\sqrt{2}$ | D. | $8+4\sqrt{2}$ |
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | $\frac{11}{2}$ |
| A. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}+{y^2}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ |
 如图,在平面直角坐标系xOy中,椭圆Ω:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.
如图,在平面直角坐标系xOy中,椭圆Ω:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.