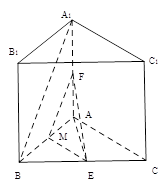
题目内容
如图，在直三棱柱中
-A BC中，AB 
AC，AB=AC=2，
=4，点D是BC的中点．
（1）求异面直线
与
所成角的余弦值；
（2）求平面
与
所成二面角的正弦值.
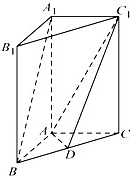
-A BC中，AB AC，AB=AC=2，=4，点D是BC的中点．（1）求异面直线
与所成角的余弦值；（2）求平面
与所成二面角的正弦值.试题分析：（1）以
为单位正交基底建立空间直角坐标系
,利用向量法能求出异面直线
与
所成角的余弦值；（2）分别求出平面
的法向量与
的法向量，利用法向量能求出平面与所成二面角的余弦值，再由三角函数知识能求出平面与所成二面角的正弦值.试题解析：（1）以
为单位正交基底建立空间直角坐标系,
则
,
,
,
,
,
.
,
异面直线与所成角的余弦值为
.（2）
是平面的的一个法向量，设平面的法向量为
,
，
，由
，
得
，取
,得
，
,所以平面
的法向量为
.设平面
与所成二面角为
.
, 得
.所以平面
与所成二面角的正弦值为
.
练习册系列答案
相关题目
中，
，
分别是
的中点，且
.
与
所成角的大小；
与平面
所成角的正弦值. 
中,
.
为平行四边形,
, 
, 
分别是
与
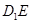的中点.
;
的平面角的余弦值.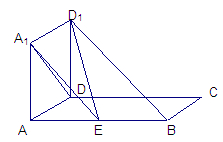
？，若存在,求出AM的长，若不存在，说明理由
中，底面
为菱形，且
为
延长线上的一点，
面
.设
.
的大小； 
上是否存在一点
，使
面
?若存在，求
的值;不存在，说明理由.
的底面为等腰直角三角形，
，
，
分别是
的中点。求异面直线
和
所成角的大小。