题目内容

已知单位向量
e1
与
e2
的夹角为60°，且
a
=2
e1
+
e2
，
b
=-3
a
+2
e2
，求
a
，
b
及
a
与
b
的夹角．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：根据向量的数量积的运算性质，求出两向量的模与夹角．
解答： 解：∵
a
=2
e1
+
e2
，
b
=-3
a
+2
e2
，且单位向量
e1
与
e2
的夹角为60°；
∴|
a
|=
4
e1
2+4
e1
•
e2
+
e2
2
=
4+4cos60°+1
=
7
，
b
=-3（2
e1
+
e2
）+2
e2
=-6
e1
-
e2
，
∴|
b
|=
36
e1
2+12
e1
•
e2
+
e2
2
=
36+12cos60°+1
=
43
；
∴
a
•
b
=-12
e1
2-2
e1
•
e2
-6
e1
•
e2
-
e2
2=-12-8cos60°-1=-17，
∴cos＜
a
，
b
＞=
a
•
b
|
a
|×|
b
|
=
-17
7
×
43
=
-17
301
301
，
∴夹角＜
a
，
b
＞=arccos（-
17
301
301
）=π-arccos
17
301
301
．
点评：本题考查了平面向量的数量积的应用问题，解题时应根据向量的运算性质，进行计算，即可得出答案，是基础题．
练习册系列答案
相关题目
已知点P（x，y）是双曲线C：x2-y2=a（a＞0）右支上动点，双曲线C的过点P的切线分别交两条渐近线于点A，B，则△OAB的面积是（　　）
A、随x的增大而增大
B、随x的增大而减小
C、a2
D、a
已知点（1，
1
3
）是函数f（x）=ax（a＞0且a≠1）的图象上一点，等比数列{an}的前n项和为f（n）-c，数列{bn}（bn＞0）的首项为c，且前n项和Sn满足Sn-Sn-1=
Sn
+
Sn-1
（n≥2）．
（1）求数列{an}、{bn}的通项公式；
（2）若数列{
1
bnbn+1
}的前n项和为Tn，问满足Tn＞
1003
2012
的最小值n是多少？
求以下的导函数：
（1）y=x2sinx；
（2）y=
lnx
ex
．
已知函数f（x）=（a+1）lnx+ax2+1．
（1）当a=-
1
3
时，求f（x）的最大值；
（2）a≤-2时，判断函数f（x）的单调性；
（3）若a≤-2，证明对任意x1，x2∈（0，+∞），均有|f（x1）-f（x2）|≥4|x1-x2|．
已知函数f（x）=
3
sinωx+cos（ωx+
π
3
）+cos（ωx-
π
3
）-1，（ω＞0，x∈R），且函数f（x）的最小正周期为π；
（1）求函数f（x）的解析式；
（2）求f（x）的单调增区间．
（3）当x∈[-
π
6
，
π
3
]时，求函数f（x）的值域．
已知a∈S，1∉S，
1
1-a
∈S，求证：1-
1
a
∈S．
设{an}是等差数列，{bn}是各项都为正数的等比数列，且满足：a1=b1=1，同时有a3+b2=5，a2+b3=6
（1）求{an}，{bn}的通项公式；
（2）求数列{
an
bn
}的前n项和Sn．
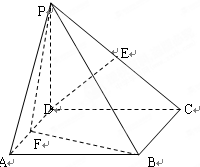如图，四棱锥P-ABCD中，四边形ABCD为正方形，PD⊥面ABCD，PD=DA=2，F，E分别为AD，PC的中点．
（1）证明：DE∥面PFB．          
（2）求点E到平面PFB的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网