题目内容
已知集合M是同时满足下列两个性质的函数f(x)组成的集合:
①f(x)在其定义域上是单调增函数或单调减函数;
②在f(x)的定义域存在区间[a,b],使得f(x)在[a,b]上的值域是[
,
].
试判断下列函数:f(x)=2x,g(x)=log2x,h(x)=x
是否属于集合M?并说明理由,若是,则请说出区间[a,b].
①f(x)在其定义域上是单调增函数或单调减函数;
②在f(x)的定义域存在区间[a,b],使得f(x)在[a,b]上的值域是[
| a |
| 2 |
| b |
| 2 |
试判断下列函数:f(x)=2x,g(x)=log2x,h(x)=x
| 1 |
| 2 |
考点:函数单调性的性质,函数奇偶性的性质
专题:函数的性质及应用
分析:分别根据函数单调性和值域之间的关系建立条件关系,即可得到结论.
解答:
 解:(1)当f(x)=2x,函数f(x)为增函数,
解:(1)当f(x)=2x,函数f(x)为增函数,
若在f(x)的定义域存在区间[a,b],使得f(x)在[a,b]上的值域是[
,
].
则
,
即a,b是方程2x=
的两个根,
由数形结合可知方程2x=
无解,故不存在满足条件的区间[a,b].
(2)当g(x)=log2x,函数g(x)为增函数,
若在g(x)的定义域存在区间[a,b],使得g(x)在[a,b]上的值域是[
,
].
则
,
即a,b是方程log2x=
的两个根,
∵x=2和x=4是方程log2x=
的根,
故a=2,b=4时满足条件,即存在满足条件的区间[2,4].
(3)当h(x)=x
,则h(x)为增函数,
∴满足条件①;
假设存在区间[a,b],使得h(x)在[a,b]上的值域是[
,
],
则
,
∴当a=0,b=4,满足条件②;
 解:(1)当f(x)=2x,函数f(x)为增函数,
解:(1)当f(x)=2x,函数f(x)为增函数,若在f(x)的定义域存在区间[a,b],使得f(x)在[a,b]上的值域是[
| a |
| 2 |
| b |
| 2 |
则
|
即a,b是方程2x=
| x |
| 2 |
由数形结合可知方程2x=
| x |
| 2 |
(2)当g(x)=log2x,函数g(x)为增函数,
若在g(x)的定义域存在区间[a,b],使得g(x)在[a,b]上的值域是[
| a |
| 2 |
| b |
| 2 |
则
|
即a,b是方程log2x=
| x |
| 2 |
∵x=2和x=4是方程log2x=
| x |
| 2 |
故a=2,b=4时满足条件,即存在满足条件的区间[2,4].
(3)当h(x)=x
| 1 |
| 2 |
∴满足条件①;
假设存在区间[a,b],使得h(x)在[a,b]上的值域是[
| a |
| 2 |
| b |
| 2 |
则
|
∴当a=0,b=4,满足条件②;
点评:本题主要考查了函数的单调性的判定和值域的求解,利用函数的单调性是解决本题的关键.同时考查了运算求解的能力和转化的思想,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
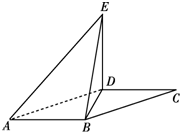 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4.将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.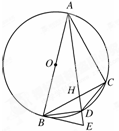 如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.