题目内容
已知0≤α≤2π,sin22α=sinα•sin4α,求α的值.
考点:二倍角的正弦
专题:三角函数的求值
分析:由题意可得 sin2α=0 ①,或sin2α=2sinα•cos2α ②.分别由①、②求得α的值,综合可得结论.
解答:
解:∵已知0≤α≤2π,sin22α=sinα•sin4α=sinα•2sin2α•cos2α,∴sin2α=0 ①,或sin2α=2sinα•cos2α ②.
由①可得2α=0,或2α=π,或2α=2π,或2α=3π,或2α=4π,求得α=0,
,π,
,2π.
由②可得 cos2α=cosα,求得cosα=1,或cosα=-
,求得α=0,或α=
.
综上可得,α的值的集合为{0,
,π,
,2π,
}.
由①可得2α=0,或2α=π,或2α=2π,或2α=3π,或2α=4π,求得α=0,
| π |
| 2 |
| 3π |
| 2 |
由②可得 cos2α=cosα,求得cosα=1,或cosα=-
| 1 |
| 2 |
| 2π |
| 3 |
综上可得,α的值的集合为{0,
| π |
| 2 |
| 3π |
| 2 |
| 2π |
| 3 |
点评:本题主要考查二倍角的正弦公式、余弦公式,根据三角函数的值求角,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
在2008奥运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲,:8,6,7,8,6,5,9,10,4,7
乙:6,7,7,8,6,7,8,7,9,5,
求出甲乙两人的平均数和方差,并分析甲、乙两人成绩.
甲,:8,6,7,8,6,5,9,10,4,7
乙:6,7,7,8,6,7,8,7,9,5,
求出甲乙两人的平均数和方差,并分析甲、乙两人成绩.
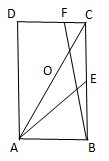 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=