题目内容
已知函数f(x)=mx2-mx-1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
考点:函数恒成立问题,二次函数的性质
专题:函数的性质及应用
分析:(1)若f(x)<0恒成立,则m=0或
,分别求出m的范围后,综合讨论结果,可得答案.
(2)若对于x∈[1,3],f(x)<5-m恒成立,则m(x-
)2+
m-6<0,x∈[1,3]恒成立,结合二次函数的图象和性质分类讨论,综合讨论结果,可得答案.
|
(2)若对于x∈[1,3],f(x)<5-m恒成立,则m(x-
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:(1)当m=0时,f(x)=-1<0恒成立,
当m≠0时,若f(x)<0恒成立,
则
解得-4<m<0
综上所述m的取值范围为(-4,0]----------------(4分)
(2)要x∈[1,3],f(x)<5-m恒成立,
即m(x-
)2+
m-6<0,x∈[1,3]恒成立.
令g(x)=m(x-
)2+
m-6,x∈[1,3]------------------------------(6分)
当m>0时,g(x)是增函数,
所以g(x)max=g(3)=7m-6<0,
解得m<
.
所以0<m<
当m=0时,-6<0恒成立.
当m<0时,g(x)是减函数.
所以g(x)min=g(1)=m-6<0,
解得m<6.
所以m<0.
综上所述,m<
-----------------------------------------------------------(12分)
当m≠0时,若f(x)<0恒成立,
则
|
解得-4<m<0
综上所述m的取值范围为(-4,0]----------------(4分)
(2)要x∈[1,3],f(x)<5-m恒成立,
即m(x-
| 1 |
| 2 |
| 3 |
| 4 |
令g(x)=m(x-
| 1 |
| 2 |
| 3 |
| 4 |
当m>0时,g(x)是增函数,
所以g(x)max=g(3)=7m-6<0,
解得m<
| 6 |
| 7 |
所以0<m<
| 6 |
| 7 |
当m<0时,g(x)是减函数.
所以g(x)min=g(1)=m-6<0,
解得m<6.
所以m<0.
综上所述,m<
| 6 |
| 7 |
点评:本题考查的知识点是函数恒成立问题,函数的最值,其中将恒成立问题转化为最值问题是解答此类问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若角α满足α=
+
(k∈Z),则α的终边一定在( )
| 2kπ |
| 3 |
| π |
| 6 |
| A、第一象限或第二象限或第三象限 |
| B、第一象限或第二象限或第四象限 |
| C、第一象限或第二象限或x轴非负半轴上 |
| D、第一象限或第二象限或y轴非正半轴上 |
如图是求
+
+
+…+
的值的程序框图,则判断框①中应填( )
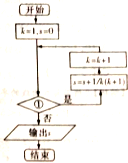
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |

| A、k≤99? |
| B、k<99? |
| C、k≤100? |
| D、k<98? |
在△ABC中,A,B,C的对边分别是a,b,c,其中a=
,b=
,sinB=
,则角A的取值范围一定属于( )
| 5 |
| 3 |
| ||
| 2 |
| A、(45°,90°) |
| B、(45°,90°)∪(90°,135°) |
| C、(0°,45°)∪(135°,180°) |
| D、(90°,135°) |
圆x2+y2-2x+4y+1=0和圆x2+y2-6x+2y+9=0的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |
执行如图所示的程序框图,如果输入的N是195,则输出的P=( )


| A、11 | B、12 | C、13 | D、14 |