题目内容
已知平面向量
=(2,-1),向量
=(1,1),向量
=(-5,1).若(
+k
)∥
,则实数k的值为 .
| a |
| b |
| c |
| a |
| b |
| c |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:由向量的数乘及坐标加法运算求得
+k
=(2+k,-1+k),然后直接利用向量共线的坐标表示列式求解k的值.
| a |
| b |
解答:
解:∵
=(2,-1),
=(1,1),
∴
+k
=(2+k,-1+k),
又
=(-5,1),
且(
+k
)∥
,
∴1×(2+k)+5(-1+k)=0,解得:k=
.
故答案为:
.
| a |
| b |
∴
| a |
| b |
又
| c |
且(
| a |
| b |
| c |
∴1×(2+k)+5(-1+k)=0,解得:k=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0,是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
相关题目
下列等式中错误的是( )
| A、sin(π+α)=-sinα |
| B、cos(π-α)=cosα |
| C、cos(2π-α)=cosα |
| D、sin(2π+α)=sinα |

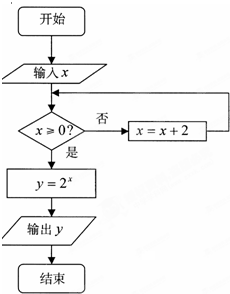 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )