题目内容
8.若定义域为R的偶函数y=f(x)满足f(x+2)=-f(x),且当x∈[0,2]时,f(x)=2-x2,则方程f(x)=sin|x|在[-3π,3π]内根的个数是10.分析 求出f(x)的周期,利用周期和对称性作出f(x)的函数图象,根据图象交点个数判断.
解答 解:∵f(x+2)=-f(x),∴f(x+4)=-f(x+2),
∴f(x+4)=f(x),即f(x)的周期为4,
作出f(x)和y=sin|x|在(0,10)上的函数图象如图所示:
由图象可知两函数图象在(0,3π)上有5个交点,即5个零点,
又f(x)与y=sin|x|都是偶函数,故在(-3π,0)上也有5个零点,
∴f(x)=sin|x|在(-3π,3π)上有10个零点.
故答案为:10.
点评 本题考查了函数的奇偶性与周期性的应用,函数零点与图象的关系,属于中档题.

练习册系列答案
相关题目
19.已知曲线C:$y=\frac{1}{3}{x^3}-{x^2}-4x+1$,直线l:x+y+2k-1=0,当x∈[-3,3]时,直线l恒在曲线C的上方,则实数k的取值范围是( )
| A. | $k>-\frac{5}{6}$ | B. | $k<-\frac{5}{6}$ | C. | $k<-\frac{3}{4}$ | D. | $k>-\frac{3}{4}$ |
20.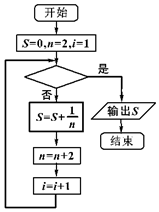 如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
 如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )| A. | i<11 | B. | i>11 | C. | i<22 | D. | i>22 |
3.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?