题目内容
已知点P是双曲线x2-
=1上的一点，F1，F2是双曲线的左右焦点，且＜
，
＞=120°，则|
+
|= ．
| y2 |
| 9 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
考点：双曲线的简单性质
专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析：由余弦定理可得4×10=m2+n2-2mncos120°，即m2+n2+mn=40，结合双曲线的定义和平面向量的数量积的定义和性质，即可得出结论．
解答：
解：由于双曲线x2-
=1，则a=1，b=3，c2=10，
设|PF1|=m，|PF2|=n，则|m-n|=2，①
由余弦定理可得4×10=m2+n2-2mncos120°，即m2+n2+mn=40，②
②-①2，可得mn=12，
∴m2+n2=40-12=28，
∴|
+
|=
=
=
=4．
故答案为：4．
| y2 |
| 9 |
设|PF1|=m，|PF2|=n，则|m-n|=2，①
由余弦定理可得4×10=m2+n2-2mncos120°，即m2+n2+mn=40，②
②-①2，可得mn=12，
∴m2+n2=40-12=28，
∴|
| PF1 |
| PF2 |
| m2+n2+2mncos120° |
| m2+n2-mn |
| 28-12 |
故答案为：4．
点评：本题主要考查了双曲线的性质，考查余弦定理以及平面向量的数量积的定义和性质，要利用好双曲线的第一定义．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
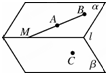如图，α∩β=l，A，B∈α，C∈β，且C∉l，直线AB∩l=M，过A，B，C三点的平面记作γ，则γ与β的交线必通过（ ）| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |