题目内容

3．椭圆$\frac{x^2}{4}$+y2=1的焦距为2$\sqrt{3}$．

分析 求出椭圆的几何量，然后求解焦距即可．

解答 解：椭圆$\frac{x^2}{4}$+y2=1的长半轴a=2，短半轴为b=1，则c=$\sqrt{4-1}$=$\sqrt{3}$．
椭圆的焦距为：2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评 本题考查椭圆的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
8．如图为某算法的程序框图，该算法的程序运行后输出的结果为299，则实数M的取值范围是（　　）
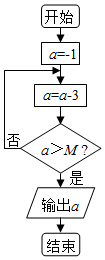
A．296＜M＜299B．296≤M＜299C．296＜M≤299D．296≤M≤299
9．已知方程$\frac{x^2}{m^2+n}$-$\frac{y^2}{3m^2-n}$=1表示双曲线，且该双曲线两焦点间的距离为4，则n的取值范围是（　　）
A．（-1，3）B．（-1，$\sqrt{3}$）C．（0，3）D．（0，$\sqrt{3}$）
6．若x，y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{x-3≤0}\end{array}\right.$，则z=x-2y的最小值为-5．
13．复数$\frac{1+2i}{2-i}$=（　　）
A．iB．1+iC．-iD．1-i
8．计算不定积分${∫}_{\;}^{\;}$（$\frac{2{x}^{2}+2x-1}{\sqrt{x}}$）dx．
15．在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，直线y=x与椭圆C交于点E，F，直线y=-x与椭圆C交于点G，H，且四边形EHFG的面积为$\frac{16}{5}$．
（1）求椭圆C的方程；
（2）过椭圆C的左顶点A作直线l1交椭圆C于另一点P，过点A作垂直于l1的直线l1，l2交椭圆C于另一点Q，当直线l1的斜率变化时，直线PQ是否过x轴上的一定点？若过定点，求出该定点的坐标，若不过定点，请说明理由．
12．复数z=（1+2i）（3-i），其中i为虚数单位，则z的实部是5．
13．△ABC的内角A，B，C的对边分别为a，b，c，若cosA=$\frac{4}{5}$，cosC=$\frac{5}{13}$，a=1，则b=$\frac{21}{13}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网