题目内容
6.已知A(-2,0),B(2,0),且△ABM的周长等于2$\sqrt{6}$+4,求动点M的轨迹G的方程:分析 设M(x,y),由题意可得|AM|+|BM|=2$\sqrt{6}$>|AB|=4,由椭圆的定义可得,M的轨迹为以A,B为焦点的椭圆(除去A,B两点),求出a,b,c,即可得到所求轨迹方程.
解答 解:设M(x,y),由题意可得
|AB|+|AM|+|BM|=2$\sqrt{6}$+4,
即为|AM|+|BM|=2$\sqrt{6}$>|AB|=4,
由椭圆的定义可得,
M的轨迹为以A,B为焦点的椭圆(除去A,B两点),
可得c=2,a=$\sqrt{6}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{2}$,
轨迹G的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(y≠0).
点评 本题考查轨迹方程的求法,注意运用椭圆的定义,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知函数f(x)=x(x-c)2在x=2处有极小值,则实数c的值为( )
| A. | 2 | B. | 2或6 | C. | 6 | D. | 4或6 |
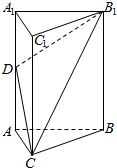 如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.
如图,三棱柱ABC-A1BC1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,D为A1A的中点.