题目内容
11．设过点P（2，2）的直线与椭圆x2+2y2=16交于A，B两点，若P为线段AB的中点，求直线AB的方程．分析 设出A，B的坐标，代入椭圆方程，利用点差法求出AB所在直线的斜率，利用直线方程的点斜式得答案．
解答 解：设A（x1，y1），B（x2，y2），
则${{x}_{1}}^{2}+2{{y}_{1}}^{2}=16$，${{x}_{2}}^{2}+2{{y}_{2}}^{2}=16$，
两式相减得${{x}_{1}}^{2}-{{x}_{2}}^{2}=-2（{{y}_{1}}^{2}-{{y}_{2}}^{2}）$，
变形可得：$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{{x}_{1}+{x}_{2}}{2（{y}_{1}+{y}_{2}）}$，
由P为线段AB的中点可知，x1+x2=4，y1+y2=4，
于是AB的斜率为-$\frac{1}{2}$，
由点斜式可得AB方程为y-2=-$\frac{1}{2}$（x-2），即x+2y-6=0．
点评 本题考查椭圆的简单性质，训练了“点差法”求中点弦的斜率，是中档题．
练习册系列答案
相关题目
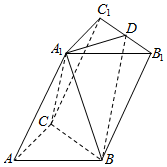如图，在三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，AA1=4，A1在底面ABC的射影为BC的中点E，D是B1C1的中点．
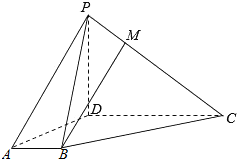如图，四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，∠BAD=$\frac{π}{3}$，AB=1，CD=3，M为PC上一点，MC=2PM．
如图，在平行六面体ABCD-A1B1C1D1中，AC与BD的交点为点M．设$\overrightarrow{{C_1}{D_1}}=\overrightarrow a$，$\overrightarrow{{C_1}{B_1}}=\overrightarrow b$，$\overrightarrow{{C_1}C}=\overrightarrow c$，用$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$表示向量$\overrightarrow{M{B_1}}$，则$\overrightarrow{M{B}_{1}}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{c}$．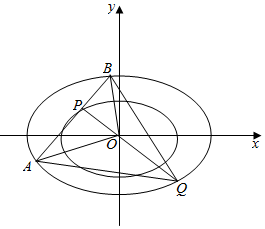
已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为4，离心率为$\frac{{\sqrt{2}}}{2}$．