题目内容
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为$\sqrt{3}$x+y=0,则其离心率e=2.分析 利用双曲线的渐近线求出ab关系,然后求解双曲线的离心率.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为$\sqrt{3}$x+y=0,
可得$\frac{b}{a}$=$\sqrt{3}$,
即$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=3$,
解得e=2.
故答案为:2.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
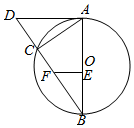 如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.
如图⊙O是Rt△ABC的外接圆,E、F是AB,BC上的点,且A,E,F,C四点共圆,延长BC至D,使得AC•BF=AD•BE.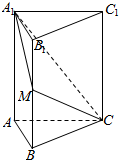 如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠ABC=90°,AB=4,AA1=6,点M时BB1中点.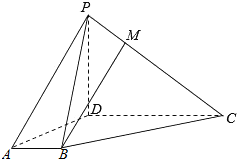 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=1,CD=3,M为PC上一点,MC=2PM.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=1,CD=3,M为PC上一点,MC=2PM.