题目内容
已知函数f(x)=
,其中a≥0.
(Ⅰ)当a=0时,求函数f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)如果对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2),求a的取值范围.
|
(Ⅰ)当a=0时,求函数f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)如果对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2),求a的取值范围.
考点:分段函数的应用
专题:综合题,函数的性质及应用
分析:(Ⅰ)当a=0时,求导函数,确定切线的斜率,求出切点的坐标,即可得到切线方程;
(Ⅱ)先考察函数g(x)=-x2+2x-3,x∈R的图象,得到a≤1;考察函数h(x)=xlnx,x∈(0,+∞)的图象,从而确定a的取值范围.
(Ⅱ)先考察函数g(x)=-x2+2x-3,x∈R的图象,得到a≤1;考察函数h(x)=xlnx,x∈(0,+∞)的图象,从而确定a的取值范围.
解答:
解:(Ⅰ)由题意,得f'(x)=(xlnx)'=lnx+1,其中x>0,…(2分)
所以 f'(1)=1,
又因为f(1)=0,
所以函数f(x)的图象在点(1,f(1))处的切线方程为y=x-1.…(4分)
(Ⅱ)先考察函数g(x)=-x2+2x-3,x∈R的图象,
配方得g(x)=-(x-1)2-2,…(5分)
所以函数g(x)在(-∞,1)上单调递增,在(1,+∞)单调递减,且g(x)max=g(1)=-2.…(6分)
因为对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2)成立,
所以a≤1.…(8分)
以下考察函数h(x)=xlnx,x∈(0,+∞)的图象,
则 h'(x)=lnx+1,
令h'(x)=lnx+1=0,解得x=
.…(9分)
随着x变化时,h(x)和h'(x)的变化情况如下:
即函数h(x)在(0,
)上单调递减,在(
, +∞)上单调递增,且h(x)min=h(
)=-
.…(11分)
因为对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2)成立,
所以 a≥
.…(12分)
因为-
>-2(即h(x)min>g(x)max),
所以a的取值范围为[
,1].…(13分)
所以 f'(1)=1,
又因为f(1)=0,
所以函数f(x)的图象在点(1,f(1))处的切线方程为y=x-1.…(4分)
(Ⅱ)先考察函数g(x)=-x2+2x-3,x∈R的图象,
配方得g(x)=-(x-1)2-2,…(5分)
所以函数g(x)在(-∞,1)上单调递增,在(1,+∞)单调递减,且g(x)max=g(1)=-2.…(6分)
因为对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2)成立,
所以a≤1.…(8分)
以下考察函数h(x)=xlnx,x∈(0,+∞)的图象,
则 h'(x)=lnx+1,
令h'(x)=lnx+1=0,解得x=
| 1 |
| e |
随着x变化时,h(x)和h'(x)的变化情况如下:
| x | (0,
|
|
(
| ||||||
| h'(x) | - | 0 | + | ||||||
| h(x) | ↘ | ↗ |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
因为对于任意x1,x2∈R,且x1<x2,都有f(x1)<f(x2)成立,
所以 a≥
| 1 |
| e |
因为-
| 1 |
| e |
所以a的取值范围为[
| 1 |
| e |
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
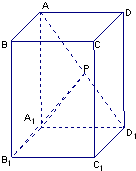 已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.