题目内容

甲乙两个兴趣小组，甲有5人，乙有7人，从这12人中选3人参加比赛，已知在甲组有1人确定参加比赛的条件下，求另外两人恰好甲乙两组各1人的概率？
考点：相互独立事件的概率乘法公式
专题：概率与统计
分析：求得另外两人恰好甲乙两组各1人的选法有4×7种，而所有的选法共有
C
2
11
 种，可得另外两人恰好甲乙两组各1人的概率．
解答： 解：由题意可得，另外两人恰好是从甲组的4人中选一个、从乙组的7人选一个组成的，
方法有4×7=28种．
而所有的选法共有
C
2
11
=55种，故另外两人恰好甲乙两组各1人的概率为
28
55
．
点评：本题主要考查古典概率及其计算公式的应用，属于基础题．
练习册系列答案
相关题目
已知点F（0，1），直线l：y=-1，P为平面上的动点，过点P作直线l的垂线，垂足为Q，且
QP
•
QF
=
FP
•
FQ
，动点P的轨迹为C，已知圆M过定点D（0，2），圆心M在轨迹C上运动，且圆M与x轴交于A、B两点，设|DA|=l1，|DB|=l2，则
l1
l2
+
l2
l1
的最大值为（　　）
A、2
B、3
C、2
2
D、3
2
在某县临时客车停靠站，每天均有上、中、下等级的客车各一辆开往城区．某天李先生准备从该站点前往城区办事，但他不知道客车的车况，也不知道发车顺序，为了尽可能乘到上等车，他采取如下策略：先放过第一辆，如果第二辆比第一辆好，则上第二辆，否则上第三辆，那么李先生乘到上等车的概率为（　　）
A、
1
3
B、
1
4
C、
1
2
D、
2
5
已知点A（1，2）在矩阵M=[
aa
1b
]（a，b，∈R）对应的变换作用下得到点A′（6，7）．
（Ⅰ）求矩阵M；
（Ⅱ）求矩阵M的特征值及属于每个特征值的一个特征向量．
已知数列{an}满足a1=2，向量
a
=（2，-1），
b
=（an+2n，an+1）且
a
⊥
b
．
（Ⅰ）求证数列{
an
2n
}为等差数列，并求{an}通项公式；
（Ⅱ）设bn=
an
n(n+1)2
，若对任意n∈N*都有bn＞
m2-3m
9
成立，求实数m的取值范围．
已知：函数f（x）=（a-2）x2+2（a-2）x-4，
（1）当a=3时，解不等式f（x）＜0；
（2）若不等式f（x）＜0的解集为R，求实数a的取值范围．
已知直线l的极坐标方程为ρ=
4
2
cos(θ+
π
4
)
，点P的直角坐标为（
3
cosθ，sinθ），求点P到直线l距离的最大值及最小值．
一场文艺晚会，有3个舞蹈，2个歌曲，4个小品，要求舞蹈和舞蹈、歌曲和歌曲不相邻，请问有多少种节目排法？
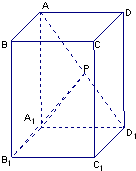已知ABCD-A1B1C1D1是底面为正方形的长方体，∠AD1A1=60°，AD1=4，点P是AD1上的动点．
（1）求证：不论点P在AD1上的任何位置，平面B1PA1都垂直于平面AA1D1
（2）当P为AD1的中点时，求异面直线AA1与B1P所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网