题目内容
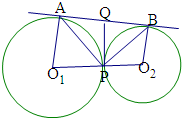
两圆外切于点P,AB是它们的一条公切线(切点为AB),若△PAB的周长为40,面积为60,则点P到AB的距离为 .
考点:圆的切线方程
专题:计算题,直线与圆
分析:作两圆的内公切线PQ,则QA=QB=QP,即有∠APB=90°,运用△APB的面积公式
PA•PB,及勾股定理,得到方程,解方程,即可得到AB=17,再由△APB的面积公式
d•AB,即可得到所求的距离.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:△PAB的周长为40,即有PA+AB+PB=40,
解:△PAB的周长为40,即有PA+AB+PB=40,
即为PA+PB=40-AB,①
作两圆的内公切线PQ,则QA=QB=QP,
即有∠APB=90°,
由三角形PAB的面积为60,即有
PA•PB=60,②
又PA2+PB2=AB2,③
①两边平方,结合②③可得,80AB=1360,
解得,AB=17.
再由△PAB的面积公式:
d•AB=60(d为P到AB的距离),
解得,d=
.
故答案为:
.
 解:△PAB的周长为40,即有PA+AB+PB=40,
解:△PAB的周长为40,即有PA+AB+PB=40,即为PA+PB=40-AB,①
作两圆的内公切线PQ,则QA=QB=QP,
即有∠APB=90°,
由三角形PAB的面积为60,即有
| 1 |
| 2 |
又PA2+PB2=AB2,③
①两边平方,结合②③可得,80AB=1360,
解得,AB=17.
再由△PAB的面积公式:
| 1 |
| 2 |
解得,d=
| 120 |
| 17 |
故答案为:
| 120 |
| 17 |
点评:本题考查两圆外切的性质,考查三角形的面积公式和运用,作两圆的内公切线PQ,即有∠APB=90°,是解题的关键.考查运算能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目