题目内容
已知二次函数y=x2+ax+a-2;
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a<0,当此函数图象与x轴的两个交点的距离为
时,求出此二次函数的解析式;
(3)若此二次函数图象与x轴交于A,B两点,在函数图象上是否存在点P,使得△PAB的面积为
,若存在,求出P点坐标;若不存在,请说明理由.
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点;
(2)设a<0,当此函数图象与x轴的两个交点的距离为
| 13 |
(3)若此二次函数图象与x轴交于A,B两点,在函数图象上是否存在点P,使得△PAB的面积为
3
| ||
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)直接计算该函数对应的一元二次方程的判别式取值情况进行证明;
(2)依据两个交点的距离为
,建立等式求解a的值;
(3)首先,假设存在这样的点,然后,根据所给的条件进行求解即可.
(2)依据两个交点的距离为
| 13 |
(3)首先,假设存在这样的点,然后,根据所给的条件进行求解即可.
解答:
解:(1)∵二次函数y=x2+ax+a-2;
∴一元二次方程x2+ax+a-2=0,
∵△=a2-4(a-2)=a2-4a+8
=(a-2)2+4>0,
∴一元二次方程x2+ax+a-2=0有两个不等实根,
∴此函数图象与x轴总有两个交点,
(2)设函数图象与x轴的两个交点的横坐标分别为x1,x2,则
x2+ax+a-2=0,
x1+x2=-a,x1x2=a-2,
∵|x1-x2|=
,
∴
=
,
∴
=
,
∴a=-1或a=5(舍去),
∴a=-1,
∴二次函数的解析式y=x2-x-3.
(3)假设存在这样的点P,满足给定的条件,
设点P(m,n),
∵|AB|=
,
∵S=
×|AB|•|n|=
,
∴|n|=3,
∴n=±3,
∴当n=3时,解得m=-2或m=3,
当n=-3时,解得m=0或m=1,
综上所述,存在这样的点,且P点坐标是(-2,3),(3,3),(0,-3)或(1,-3).
∴一元二次方程x2+ax+a-2=0,
∵△=a2-4(a-2)=a2-4a+8
=(a-2)2+4>0,
∴一元二次方程x2+ax+a-2=0有两个不等实根,
∴此函数图象与x轴总有两个交点,
(2)设函数图象与x轴的两个交点的横坐标分别为x1,x2,则
x2+ax+a-2=0,
x1+x2=-a,x1x2=a-2,
∵|x1-x2|=
| 13 |
∴
| (x1+x2)2-4x1x2 |
| 13 |
∴
| a2-4(a-2) |
| 13 |
∴a=-1或a=5(舍去),
∴a=-1,
∴二次函数的解析式y=x2-x-3.
(3)假设存在这样的点P,满足给定的条件,
设点P(m,n),
∵|AB|=
| 13 |
∵S=
| 1 |
| 2 |
3
| ||
| 2 |
∴|n|=3,
∴n=±3,
∴当n=3时,解得m=-2或m=3,
当n=-3时,解得m=0或m=1,
综上所述,存在这样的点,且P点坐标是(-2,3),(3,3),(0,-3)或(1,-3).
点评:本题重点考查了二次函数的图象与性质、存在性问题的处理思路和方法,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列函数中,值域为R的是( )
A、f(x)=
| ||
| B、f(x)=2x | ||
| C、f(x)=ln(x2+1) | ||
| D、f(x)=lg(x+1) |
设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩∁UM=( )
| A、{0} | B、{1} |
| C、{-1,-2,0} | D、∅ |
已知复数z=(1+i)(2-i)(i为虚数单位),则|z|=( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知集合A={x|x-2=0},B={0,1,2},则A∩B=( )
| A、{0} | B、{0,1,} |
| C、{2} | D、{0,1,2} |
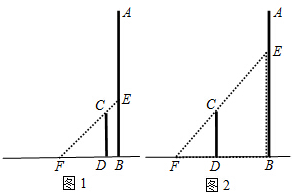 如图所示,直立在地面上的两根钢管AB和CD,AB=10
如图所示,直立在地面上的两根钢管AB和CD,AB=10