题目内容
7．某三棱锥的三视图如图所示，则其外接球的表面积为$\frac{32π}{3}$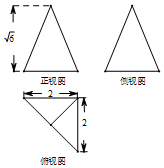
分析 由已知可得该几何体的是一个以俯视图为底面的三棱锥，球心在棱锥的高上，且R2=（h-R）2+r2，进而可得答案．
解答 解：由已知可得该几何体的是一个以俯视图为底面的三棱锥，
其底面是一个边长为2的等腰直角三角形，
故底面半径r=$\sqrt{2}$，
棱锥的高h=$\sqrt{6}$，球心在棱锥的高上，
且R2=（h-R）2+r2，
即R=$\frac{2\sqrt{6}}{3}$，
故外接球的表面积S=4πR2=$\frac{32π}{3}$，
故答案为：$\frac{32π}{3}$
点评 本题考查的知识点是球内接多面体，球的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
2．为了普及法律知识，达到“法在心中”的目的，某市法制办组织了一次普法知识竞赛．统计局调查队从甲、乙两单位中各随机抽取了5名职工的成绩，如下：
（1）根据表中的数据，分别求出样本中甲、乙两单位职工成绩的平均数和方差，并判断哪个单位职工对法律知识的掌握更为稳定；
（2）用简单随机抽样的方法从乙单位的5名职工中抽取2名，他们的成绩组成一个样本，求抽取的2名职工的成绩之差的绝对值至少是4分的概率．
| 甲单位职工的成绩（分） | 87 | 88 | 91 | 91 | 93 |
| 乙单位职工的成绩（分） | 85 | 89 | 91 | 92 | 93 |
（2）用简单随机抽样的方法从乙单位的5名职工中抽取2名，他们的成绩组成一个样本，求抽取的2名职工的成绩之差的绝对值至少是4分的概率．
16．设x∈[0，3]，执行如图所示的程序框图，从输出的结果中随机取一个数a，则“a≤5”的概率为（ ）
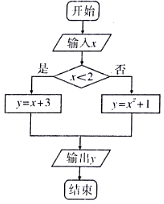
| A． | $\frac{2}{3}$ | B． | $\frac{5}{6}$ | C． | $\frac{2}{7}$ | D． | $\frac{5}{7}$ |