题目内容
18.若(x-$\frac{2}{x}$)n的展开式中第二项与第四项的二项式系数相等,则直线y=nx与曲线y=x2围成的封闭图形的面积为$\frac{32}{3}$.分析 先确定n的值,再求出直线y=nx与曲线y=x2交点坐标,利用定积分求得直线y=nx与曲线y=x2围成图形的面积.
解答 解:∵(x-$\frac{2}{x}$)n的展开式中第2项与第4项的二项式系数相等,
∴Cn1=Cn3,
∴n=4,
由直线y=4x与曲线y=x2,可得交点坐标为(0,0),(4,16),
∴直线y=nx与曲线y=x2围成的封闭区域面积为${∫}_{0}^{4}$(4x-x2)dx=(2x2-$\frac{1}{3}$x3)|${\;}_{0}^{4}$=$\frac{32}{3}$.
故答案为:$\frac{32}{3}$
点评 本题主要考查二项式定理的应用,利用定积分求曲边形的面积,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设△ABC的面积为S1,它的外接圆面积为S2,若△ABC的三个内角大小满足A:B:C=3:4:5,则$\frac{{S}_{1}}{{S}_{2}}$的值为( )
| A. | $\frac{25}{12π}$ | B. | $\frac{25}{24π}$ | C. | $\frac{3+\sqrt{3}}{2π}$ | D. | $\frac{3+\sqrt{3}}{4π}$ |
6.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{ax,x<0}\end{array}\right.$若方程f(-x)=f(x)有五个不同的根,则实数a的取值范围为( )
| A. | (-∞,-e) | B. | (-∞,-1) | C. | (1,+∞) | D. | (e,+∞) |
8.已知集合A={-3,-2,-1},B={x∈Z|-2≤x≤1},则A∪B=( )
| A. | {-1} | B. | {-2,-1} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1,0,1} |

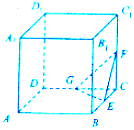 如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别是棱BC,CC1,CD的中点,平面α过点B1且与平面EFG平行,则平面α被该正方体外接球所截得的截面圆的面积为为$\frac{2}{3}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别是棱BC,CC1,CD的中点,平面α过点B1且与平面EFG平行,则平面α被该正方体外接球所截得的截面圆的面积为为$\frac{2}{3}π$.