题目内容
8.已知5件产品中有2件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为ξ,则Eξ=( )| A. | 3 | B. | $\frac{7}{2}$ | C. | $\frac{18}{5}$ | D. | 4 |
分析 由题意知ξ的可能取值为2,3,4,分别求出相应的概率,由此能求出Eξ.
解答 解:由题意知ξ的可能取值为2,3,4,
P(ξ=2)=$\frac{2}{5}×\frac{1}{4}$=$\frac{1}{10}$,
P(ξ=3)=$\frac{2}{5}×\frac{3}{4}×\frac{1}{3}$+$\frac{3}{5}×\frac{2}{4}×\frac{1}{3}$+$\frac{3}{5}×\frac{2}{4}×\frac{1}{3}$=$\frac{3}{10}$,
P(ξ=4)=1-$\frac{1}{10}-\frac{3}{10}$=$\frac{6}{10}$,
∴Eξ=$2×\frac{1}{10}+3×\frac{3}{10}+4×\frac{6}{10}$=$\frac{7}{2}$.
故选:B.
点评 本题离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知数列{an}的前n项和为Sn,且Sn=n-5an+23,n∈N*,则数列{an}的通项公式an=( )
| A. | $3×{(\frac{5}{6})^{n-1}}-1$ | B. | $3×{(\frac{5}{6})^n}-1$ | C. | $3×{(\frac{5}{6})^{n-1}}+1$ | D. | $3×{(\frac{5}{6})^n}+1$ |
17.某几何体的三视图如图所示,则该几何体的表面积为( )
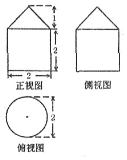

| A. | $\frac{7π}{3}$ | B. | $8+\frac{π}{3}$ | C. | $({4+\sqrt{2}})π$ | D. | $({5+\sqrt{2}})π$ |
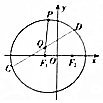 一张半径为4的圆形纸片的圆心为F1,F2是圆内一个定点,且F1F2=2,P是圆上一个动点,把纸片折叠使得F2与P重合,然后抹平纸片,折痕为CD,设CD与半径PF1的交点为Q,当P在圆上运动时,则Q点的轨迹为曲线E,以F1F2所在直线x为轴,F1F2的中垂线为y轴建立平面直角坐标系,如图.
一张半径为4的圆形纸片的圆心为F1,F2是圆内一个定点,且F1F2=2,P是圆上一个动点,把纸片折叠使得F2与P重合,然后抹平纸片,折痕为CD,设CD与半径PF1的交点为Q,当P在圆上运动时,则Q点的轨迹为曲线E,以F1F2所在直线x为轴,F1F2的中垂线为y轴建立平面直角坐标系,如图.