题目内容
13.已知数列{an}的前n项和为Sn,且Sn=n-5an+23,n∈N*,则数列{an}的通项公式an=( )| A. | $3×{(\frac{5}{6})^{n-1}}-1$ | B. | $3×{(\frac{5}{6})^n}-1$ | C. | $3×{(\frac{5}{6})^{n-1}}+1$ | D. | $3×{(\frac{5}{6})^n}+1$ |
分析 Sn=n-5an+23,n∈N*,当n=1时,a1=S1=1-5a1+23,解得a1.n≥2时,an=Sn-Sn-1,化为an-1=$\frac{5}{6}$(an-1-1),再利用等比数列的通项公式即可得出.
解答 解:∵Sn=n-5an+23,n∈N*,
∴当n=1时,a1=S1=1-5a1+23,解得a1=4.
n≥2时,an=Sn-Sn-1=n-5an+23-(n-1-5an-1+23),化为:an-1=$\frac{5}{6}$(an-1-1),a1-1=3.
∴数列{an-1}是等比数列,首项为3,公比为$\frac{5}{6}$.
∴an-1=$3×(\frac{5}{6})^{n-1}$,即an=$3×(\frac{5}{6})^{n-1}$+1,
故选:C.
点评 本题考查了数列递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
4.某校高三年级准备举行一次座谈会,其中三个班被邀请的学生数如表所示:
(Ⅰ)若从这10名学生中随机选出2名学生发言,求这2名学生不属于同一班级的概率;
(Ⅱ)若从这10名学生中随机选出3名学生发言,设X为来自高三(1)班的学生人数,求随机变量X的分布列和数学期望.
| 班级 | 高三(1) | 高三(2) | 高三(3) |
| 人数 | 3 | 3 | 4 |
(Ⅱ)若从这10名学生中随机选出3名学生发言,设X为来自高三(1)班的学生人数,求随机变量X的分布列和数学期望.
8.已知5件产品中有2件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为ξ,则Eξ=( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | $\frac{18}{5}$ | D. | 4 |
18.连续掷两次骰子,以先后得到的点数m,n为点P的坐标(m,n),那么点P在圆x2+y2=17内部(不包括边界)的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{18}$ | D. | $\frac{2}{9}$ |
5.$\frac{sin10°}{1-\sqrt{3}tan10°}$=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
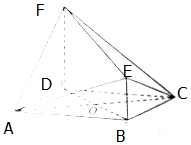 如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.
如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3.